所有小学数学公式大全
数学日记:分数和小数
带分数、带分数、分数和小数
一些小数可以等于一些真分数或假分数,假分数又可以等于带分数或整数,也就是小数=假分数=带分数(整数),或小数=真分数,举些例子来说说:(1)0.75=
753=75%=1004
把小数化成分数很容易,只要
整数部分是0,再把小数扩大成整数,扩大多少倍,那倍数就是分母,小数扩大成的整数就是分子。变成了这么大的分数后,只要再看看它能不能分子、分母同时除以一个不等于0的数,数分大小不变,这个小数就变成了分数了。(2)
14=14÷20=0.720
分数化小数也不难,只要用
分数的分子去除以分母(不管是真分数还是假分数),就可以得到小数了,得到的小数就是你要化的小数了。这里又有一个新知识,就是分子相当于被除数,分数线相当于除号,分母相当于除数。(3)8.96=8
96÷424=8100÷425
这个小数跟上面的不同了一
点它有整数。看起来不好化分,其实很好化分。整数不用化分,只用化分小数,小数化分完后再加上整数,就化分好了,化分出来的是一个带分数。在一个除法算式里,当被除数不能被除数除尽时商就可以用分数表示,就是分子=被除数,分数线=除号,分母=除数。
这几天,钱老师为了让我们更快一步算出一些题目的结果,教我们除、乘法的简便算法。我心想:竖式计算我也很快。难道还有别的方法可以让计算更快捷吗?我带着满脑子的疑问认真听钱老师讲课,终于明白了其中的道理。原来,要简便运算还要先弄懂乘除法的根据。乘法根据是:三个数相乘,可以先把后面两个数相乘,再和第一个数相乘,结果不变。除法根据是:一个数连续用两个数除,每次都能除尽的时候,可以先把这两个数相乘,用它们的积去除这个数,结果不变。我来举一个例子说吧:25×16=25×4×4,=100×4,=400怎么样?这个算式如果用竖式计算还要花大约一分钟的时间,可这个算式如果用简便算法来做的话,很快就可以算出结果来了。在我简便计算刚学不久时,爸爸给我出了一道题,我一下子就回答出来了,我是这样计算的:35×12=35×2×6=70×6=420,爸爸听了我的回答,表扬了我。我告诉你们一个小知识:后面带有5的数,最好找一个和这个数相乘得整十或整百的数来相乘。
简便算法很容易吧!
小数形式时需要注意什么
一、化简下面的小数:
2.00=1.4000=0.050=0.800=
40.040=10.000=4.070=59.30200=
5.40=15.050=2.700=10.800=
0.100=0.0710=110.00=0.8090=
0.80=3.500=15.000=1.640=
0.070=10.030=0.050=4.080=
6.230=6.000=8.020=7.00=
二、不改变数的大小,把下面的各数写成三位小数
0.8=3.0700=13=6.24=
5.45=2.7=8.4000=10.7=
0.5=25=9.4000=47=
2.04=30.5=10=2.4=
305=10.1=11.5=0.07=
三、在括号填上适当的“<”“>”或“=”
3.012.999.449.463.5673.576
15.60()1510.99910.10
7.37.91.351.3506.586.85
6.78.20.090.17.47.14
数学所有图形的周长面积体积表面积公式
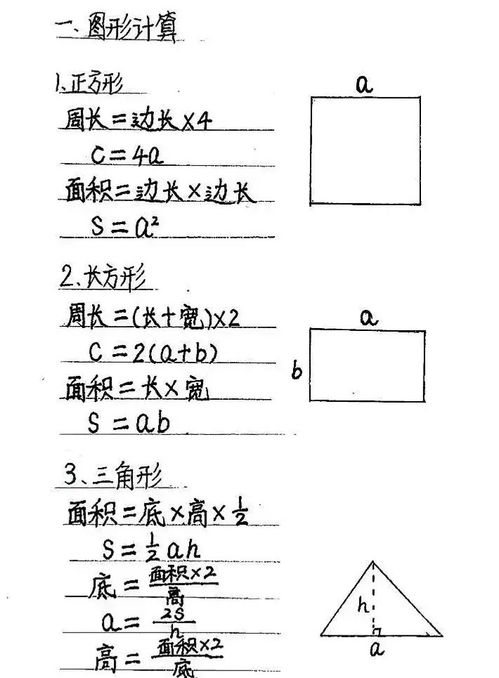
小学数学图形计算公式
平面图形图形名称图形周长(C)公式面积(S)公式正方形(4条对称轴)a周长=边长×4C=4a公式变换:a=C÷4=C面积=边长×边长S=a×a=a2长方形(2条对称轴)ba周长=长+长+宽+宽=2长+2宽=(长+宽)×2C=(a+b)×2公式变换:a=C÷2-bb=C÷2-a面积=长×宽S=a×b=ab公式变换:a=S÷bb=S÷a三角形(等边△有3条对称轴;等腰△有1条对称轴)cbhaa周长=边长a+边长b+边长cC=a+b+c注:等边△周长C=3a公式变换:a=C÷3面积=底×高÷2s=ah÷2=ah公式变换:三角形高=面积×2÷底h=2s÷a三角形底=面积×2÷高a=2s÷h平行四边形(没有对称轴)ahaab周长=边长a+边长a+边长b+边长b=边长a×2+边长b×2C=2a+2b=2(a+b)面积=底×高s=ah公式变换:a=s÷hh=s÷a梯形(等腰梯形有1条对称轴)haedb周长=边长a+边长b+边长d+边长eC=a+b+d+e面积=(上底+下底)×高÷2s=(a+b)×h÷2公式变换:a=2s÷h-bb=2s÷h-a圆形rd周长=直径×π=2×π×半径C=πd=2πr公式变换:d=2rr=d÷2d=C÷πr=C÷2π※半圆周长=πr+d面积=半径×半径×πS=πr2圆环周长=C大圆+C小圆=πD+πd=2πR+2πr=2π(R+r)面积=S大圆-S小圆=πR2-πr2=π(R2-r2)立体图形图形名称图形总棱长(L)公式表面积(S)公式体(容)积(V)公式正方体a总棱长=棱长×12L=12aS=一个面的面积×6S=a×a×6=6a2体积=棱长×棱长×棱长V=a×a×a=a3长方体hba总棱长=长×4+宽×4+高×4=4(长+宽+高)L=4(a+b+h)表面积=(长×宽+长×高+宽×高)×2S=2(ab+ah+bh)体积=长×宽×高V=abh圆柱体侧面积=底面周长×高S侧=ch=dπh=2πrh表面积=底面积×2+侧面积S表=S底×2+S侧圆柱的表面积公式:(1)有两个底面的圆柱的表面积公式:S表=S底×2+S侧=πr2×2+πdh=πr2×2+2πrh=2πr(r+h)(2)只有1个底面的圆柱的表面积公式:S表=S底+S侧=πr2+πdh=πr2+2πrh=πr(r+2h)(3)两个底面都没有的圆柱的表面积公式:S表=S侧=ch=πdh=2πrh体积=底面积×高=侧面积÷2×半径V=S底×h=πr2h圆筒大圆柱直径为D,半径为R,周长为C;小圆柱直径为d,半径为r,周长为c;高都为hS表=S大圆柱侧+S小圆柱侧+(S大圆柱底-S小圆柱底)×2=C大圆柱h+c小圆柱h+(πR2-πr2)×2=Dπh+dπh+(πR2-πr2)×2=πh(D+d)+2π(R2-r2)=2πh(R+r)+2π(R2-r2)V=V大圆柱-V小圆柱=S大圆柱底×h-S小圆柱底×h=πR2h-πr2×h=πh(R2-r2)圆锥体体积=底面积×高÷3V圆锥=V圆柱=S底×h=πr2hV圆柱=3V圆锥等底等体积的圆柱与圆锥,圆锥的高=圆柱高的3倍
数学与生活的小报资料
——数学小知识
1、阿拉伯数字
在生活中,我们经常会用到0、1、2、3、4、5、6、7、8、9这些数字,数学小报资料。那么你知道这些数字是谁发明的吗
这些数字符号原来是古代印度人发明的,后来传到阿拉伯,又从阿拉伯传到欧洲,欧洲人误以为是阿拉伯人发明的,就把它们叫做“阿拉伯数字”,因为流传了许多年,人们叫得顺口,所以至今人们仍然将错就错,把这些古代印度人发明的数字符号叫做阿拉伯数字。
现在,阿拉伯数字已成了全世界通用的数字符号。
2、九九歌
九九歌就是我们现在使用的乘法口诀。
远在公元前的春秋战国时代,九九歌就已经被人们广泛使用。在当时的许多著作中,都有关于九九歌的记载。最初的九九歌是从“九九八十一”起到“二二如四”止,共36句。因为是从“九九八十一”开始,所以取名九九歌。大约在公元五至十世纪间,九九歌才扩充到“一一如一”。大约在公元十三、十四世纪,九九歌的顺序才变成与现在所用的一样,从“一一如一”起到“九九八十一”止。
现在我国使用的乘法口诀有两种,一种是45句的,通常称为“小九九”;还有一种是81句的,通常称为“大九九”。
数学公示和定律
小学数学公式:
1、长方形的周长=(长+宽)×2C=(a+b)×2
2、正方形的周长=边长×4C=4a
3、长方形的面积=长×宽S=ab
4、正方形的面积=边长×边长S=a.a=a
5、三角形的面积=底×高÷2S=ah÷2
6、平行四边形的面积=底×高S=ah
7、梯形的面积=(上底+下底)×高÷2S=(a+b)h÷2
8、直径=半径×2d=2r半径=直径÷2r=d÷2
9、圆的周长=圆周率×直径=圆周率×半径×2c=πd=2πr
10、圆的面积=圆周率×半径×半径?=πr
11、长方体的表面积=(长×宽+长×高+宽×高)×2
12、长方体的体积=长×宽×高V=abh
13、正方体的表面积=棱长×棱长×6S=6a
14、正方体的体积=棱长×棱长×棱长V=a.a.a=a
15、圆柱的侧面积=底面圆的周长×高S=ch
16、圆柱的表面积=上下底面面积+侧面积
S=2πr+2πrh=2π(d÷2)+2π(d÷2)h=2π(C÷2÷π)+Ch
17、圆柱的体积=底面积×高V=Sh
V=πrh=π(d÷2)h=π(C÷2÷π)h
18、圆锥的体积=底面积×高÷3
V=Sh÷3=πrh÷3=π(d÷2)h÷3=π(C÷2÷π)h÷3
19、长方体(正方体、圆柱体)的体
1、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数
2、1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数
3、速度×时间=路程路程÷速度=时间路程÷时间=速度
4、单价×数量=总价总价÷单价=数量总价÷数量=单价
5、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率
6、加数+加数=和和-一个加数=另一个加数
7、被减数-减数=差被减数-差=减数差+减数=被减数
8、因数×因数=积积÷一个因数=另一个因数
9、被除数÷除数=商被除数÷商=除数商×除数=被除数
小学数学图形计算公式
1、正方形C周长S面积a边长周长=边长×4C=4a面积=边长×边长S=a×a
2、正方体V:体积a:棱长表面积=棱长×棱长×6S表=a×a×6体积=棱长×棱长×棱长V=a×a×a
3、长方形
C周长S面积a边长
周长=(长+宽)×2
C=2(a+b)
面积=长×宽
S=ab
4、长方体
V:体积s:面积a:长b:宽h:高
(1)表面积(长×宽+长×高+宽×高)×2
S=2(ab+ah+bh)
(2)体积=长×宽×高
V=abh
5三角形
s面积a底h高
面积=底×高÷2
s=ah÷2
三角形高=面积×2÷底
三角形底=面积×2÷高
6平行四边形
s面积a底h高
面积=底×高
s=ah
7梯形
s面积a上底b下底h高
面积=(上底+下底)×高÷2
s=(a+b)×h÷2
8圆形
S面积C周长∏d=直径r=半径
(1)周长=直径×∏=2×∏×半径
C=∏d=2∏r
(2)面积=半径×半径×∏
9圆柱体
v:体积h:高s;底面积r:底面半径c:底面周长
(1)侧面积=底面周长×高
(2)表面积=侧面积+底面积×2
(3)体积=底面积×高
(4)体积=侧面积÷2×半径
10圆锥体
v:体积h:高s;底面积r:底面半径
体积=底面积×高÷3
总数÷总份数=平均数
和差问题
(和+差)÷2=大数
(和-差)÷2=小数
和倍问题
和÷(倍数-1)=小数
小数×倍数=大数
(或者和-小数=大数)
差倍问题
差÷(倍数-1)=小数
小数×倍数=大数
(或小数+差=大数)
植树问题
1非封闭线路上的植树问题主要可分为以下三种情形:
⑴如果在非封闭线路的两端都要植树,那么:
株数=段数+1=全长÷株距-1
全长=株距×(株数-1)
株距=全长÷(株数-1)
⑵如果在非封闭线路的一端要植树,另一端不要植树,那么:
株数=段数=全长÷株距
全长=株距×株数
株距=全长÷株数
⑶如果在非封闭线路的两端都不要植树,那么:
株数=段数-1=全长÷株距-1
全长=株距×(株数+1)
株距=全长÷(株数+1)
2封闭线路上的植树问题的数量关系如下
株数=段数=全长÷株距
全长=株距×株数
株距=全长÷株数
盈亏问题
(盈+亏)÷两次分配量之差=参加分配的份数
(大盈-小盈)÷两次分配量之差=参加分配的份数
(大亏-小亏)÷两次分配量之差=参加分配的份数
相遇问题
相遇路程=速度和×相遇时间
相遇时间=相遇路程÷速度和
速度和=相遇路程÷相遇时间
追及问题
追及距离=速度差×追及时间
追及时间=追及距离÷速度差
速度差=追及距离÷追及时间
流水问题
顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
静水速度=(顺流速度+逆流速度)÷2
水流速度=(顺流速度-逆流速度)÷2
浓度问题
溶质的重量+溶剂的重量=溶液的重量
溶质的重量÷溶液的重量×100%=浓度
溶液的重量×浓度=溶质的重量
溶质的重量÷浓度=溶液的重量
利润与折扣问题
利润=售出价-成本
利润率=利润÷成本×100%=(售出价÷成本-1)×100%
涨跌金额=本金×涨跌百分比
折扣=实际售价÷原售价×100%(折扣<1)
利息=本金×利率×时间
税后利息=本金×利率×时间×(1-20%)
时间单位换算
1世纪=100年1年=12月
大月(31天)有:135781012月
小月(30天)的有:46911月
平年2月28天,闰年2月29天
平年全年365天,闰年全年366天
1日=24小时1时=60分
1分=60秒1时=3600秒积=底面积×高V=Sh
1.认识圆柱和圆锥,掌握它们的基本特征。认识圆柱的底面、侧面和高。认识圆锥的底面和高。通过对圆柱和圆锥的认识,牢记圆柱的表面积,圆柱的体积和圆锥的体积。
2.探索并掌握圆柱的侧面积、表面积的计算方法,以及圆柱、圆锥体积的计算公式,会运用公式计算体积,解决有关的简单实际问题。
3.通过观察、设计和制作圆柱、圆锥模型等活动,了解平面图形与立体图形之间的联系,发展学生的空间观念。
正方形的面积为边长的平方,周长为4边长
长方形的面积为长乘宽,周长为2(长+宽)
平行四边形的面积为长乘高,周长为2×临边的和
梯形的面积为(上底+下底)乘高÷2,周长为各边之和
三角形的面积为底乘高除以2,周长为各边之和
圆柱的面积为侧面积加上底面两圆面积之和,等于底面周长乘以高加2πr^2
圆锥的面积为扇形面积加底面积,等于底面周长乘以母线长除以2,或nπR^2除以360
体积和表面积
三角形的面积=底×高÷2。公式S=a×h÷2
正方形的面积=边长×边长公式S=a2
长方形的面积=长×宽公式S=a×b
平行四边形的面积=底×高公式S=a×h
梯形的面积=(上底+下底)×高÷2公式S=(a+b)h÷2
内角和:三角形的内角和=180度。
长方体的表面积=(长×宽+长×高+宽×高)×2公式:S=(a×b+a×c+b×c)×2
正方体的表面积=棱长×棱长×6公式:S=6a2
长方体的体积=长×宽×高公式:V=abh
长方体(或正方体)的体积=底面积×高公式:V=abh
正方体的体积=棱长×棱长×棱长公式:V=a3
圆的周长=直径×π公式:L=πd=2πr
圆的面积=半径×半径×π公式:S=πr2
圆柱的表(侧)面积:圆柱的表(侧)面积等于底面的周长乘高。公式:S=ch=πdh=2πrh
圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积。公式:S=ch+2s=ch+2πr2
圆柱的体积:圆柱的体积等于底面积乘高。公式:V=Sh
圆锥的体积=1/3底面×积高。公式:V=1/3Sh
算术
1、加法交换律:两数相加交换加数的位置,和不变。
2、加法结合律:a+b=b+a
3、乘法交换律:a×b=b×a
4、乘法结合律:a×b×c=a×(b×c)
5、乘法分配律:a×b+a×c=a×b+c
6、除法的性质:a÷b÷c=a÷(b×c)
7、除法的性质:在除法里,被除数和除数同时扩大(或缩小)相同的倍数,商不变。O除以任何不是O的数都得O。简便乘法:被乘数、乘数末尾有O的乘法,可以先把O前面的相乘,零不参加运算,有几个零都落下,添在积的末尾。
8、有余数的除法:被除数=商×除数+余数
方程、代数与等式
等式:等号左边的数值与等号右边的数值相等的式子叫做等式。等式的基本性质:等式两边同时乘以(或除以)一个相同的数,等式仍然成立。
方程式:含有未知数的等式叫方程式。
一元一次方程式:含有一个未知数,并且未知数的次数是一次的等式叫做一元一次方程式。学会一元一次方程式的例法及计算。即例出代有χ的算式并计算。
代数:代数就是用字母代替数。
代数式:用字母表示的式子叫做代数式。如:3x=ab+c
分数
分数:把单位“1”平均分成若干份,表示这样的一份或几分的数,叫做分数。
分数大小的比较:同分母的分数相比较,分子大的大,分子小的小。异分母的分数相比较,先通分然后再比较;若分子相同,分母大的反而小。
分数的加减法则:同分母的分数相加减,只把分子相加减,分母不变。异分母的分数相加减,先通分,然后再加减。
分数乘整数,用分数的分子和整数相乘的积作分子,分母不变。
分数乘分数,用分子相乘的积作分子,分母相乘的积作为分母。
分数的加、减法则:同分母的分数相加减,只把分子相加减,分母不变。异分母的分数相加减,先通分,然后再加减。
倒数的概念:1.如果两个数乘积是1,我们称一个是另一个的倒数。这两个数互为倒数。1的倒数是1,0没有倒数。
分数除以整数(0除外),等于分数乘以这个整数的倒数。
分数的基本性质:分数的分子和分母同时乘以或除以同一个数(0除外),分数的大小
分数的除法则:除以一个数(0除外),等于乘这个数的倒数。
真分数:分子比分母小的分数叫做真分数。
假分数:分子比分母大或者分子和分母相等的分数叫做假分数。假分数大于或等于1。
带分数:把假分数写成整数和真分数的形式,叫做带分数。
分数的基本性质:分数的分子和分母同时乘以或除以同一个数(0除外),分数的大小不变。
数量关系计算公式
单价×数量=总价2、单产量×数量=总产量
速度×时间=路程4、工效×时间=工作总量
加数+加数=和一个加数=和+另一个加数
被减数-减数=差减数=被减数-差被减数=减数+差
因数×因数=积一个因数=积÷另一个因数
被除数÷除数=商除数=被除数÷商被除数=商×除数
长度单位:
1公里=1千米1千米=1000米
1米=10分米1分米=10厘米1厘米=10毫米
面积单位:
1平方千米=100公顷1公顷=10000平方米
1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米
1亩=666.666平方米。
体积单位
1立方米=1000立方分米1立方分米=1000立方厘米
1立方厘米=1000立方毫米
1升=1立方分米=1000毫升1毫升=1立方厘米
重量单位
1吨=1000千克1千克=1000克=1公斤=1市斤
比
什么叫比:两个数相除就叫做两个数的比。如:2÷5或3:6或1/3比的前项和后项同时乘以或除以一个相同的数(0除外),比值不变。
什么叫比例:表示两个比相等的式子叫做比例。如3:6=9:18
比例的基本性质:在比例里,两外项之积等于两内项之积。
解比例:求比例中的未知项,叫做解比例。如3:χ=9:18
正比例:两种相关联的量,一种量变化,另一种量也随着化,如果这两种量中相对应的的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系。如:y/x=k(k一定)或kx=y
反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关系。如:x×y=k(k一定)或k/x=y
百分数
百分数:表示一个数是另一个数的百分之几的数,叫做百分数。百分数也叫做百分率或百分比。
把小数化成百分数,只要把小数点向右移动两位,同时在后面添上百分号。其实,把小数化成百分数,只要把这个小数乘以100%就行了。把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位。
把分数化成百分数,通常先把分数化成小数(除不尽时,通常保留三位小数),再把小数化成百分数。其实,把分数化成百分数,要先把分数化成小数后,再乘以100%就行了。
把百分数化成分数,先把百分数改写成分数,能约分的要约成最简分数。
要学会把小数化成分数和把分数化成小数的化发。
倍数与约数
最大公约数:几个数公有的约数,叫做这几个数的公约数。公因数有有限个。其中最大的一个叫做这几个数的最大公约数。
最小公倍数:几个数公有的倍数,叫做这几个数的公倍数。公倍数有无限个。其中最小的一个叫做这几个数的最小公倍数。
互质数:公约数只有1的两个数,叫做互质数。相临的两个数一定互质。两个连续奇数一定互质。1和任何数互质。
通分:把异分母分数的分别化成和原来分数相等的同分母的分数,叫做通分。(通分用最小公倍数)
约分:把一个分数的分子、分母同时除以公约数,分数值不变,这个过程叫约分。
最简分数:分子、分母是互质数的分数,叫做最简分数。分数计算到最后,得数必须化成最简分数。
质数(素数):一个数,如果只有1和它本身两个约数,这样的数叫做质数(或素数)。
合数:一个数,如果除了1和它本身还有别的约数,这样的数叫做合数。1不是质数,也不是合数。
质因数:如果一个质数是某个数的因数,那么这个质数就是这个数的质因数。
分解质因数:把一个合数用质因数相成的方式表示出来叫做分解质因数。
倍数特征:
2的倍数的特征:各位是0,2,4,6,8。
3(或9)的倍数的特征:各个数位上的数之和是3(或9)的倍数。
5的倍数的特征:各位是0,5。
4(或25)的倍数的特征:末2位是4(或25)的倍数。
8(或125)的倍数的特征:末3位是8(或125)的倍数。
7(11或13)的倍数的特征:末3位与其余各位之差(大-小)是7(11或13)的倍数。
17(或59)的倍数的特征:末3位与其余各位3倍之差(大-小)是17(或59)的倍数。
19(或53)的倍数的特征:末3位与其余各位7倍之差(大-小)是19(或53)的倍数。
23(或29)的倍数的特征:末4位与其余各位5倍之差(大-小)是23(或29)的倍数。
倍数关系的两个数,最大公约数为较小数,最小公倍数为较大数。
互质关系的两个数,最大公约数为1,最小公倍数为乘积。
两个数分别除以他们的最大公约数,所得商互质。
两个数的与最小公倍数的乘积等于这两个数的乘积。
两个数的公约数一定是这两个数最大公约数的约数。
1既不是质数也不是合数。
用6去除大于3的质数,结果一定是1或5。
数学小报内容
趣味数学知识(一)
一、最小的数字。
古老而庞大的自然数家族,是由全体自然数1、2、3、4、5、6、7、8、9、10……集合在一起组成的。其中最小的是“1”,找不到最大的。如果你有兴趣的话,可以找一找。
二、没有最大的自然数。
也许你认为可以找到一个最大的自然数(n),但是,你立刻就会发现另一个自然数(n+1),它大于n。这就说明在自然数家族中永远找不到最大的自然数。
三、“1”确实是自然数家族中最小的。
自然数是无限的,而“1”是自然数中最小的。有人提出异议,不同意“1”是最小的自然数,说“0”比“1”小,“0”应该是最小的自然数。这是不对的,因为自然数指的是正整数,“0”是唯一的非正非负的整数,因而“0”不属于自然数家族。“1”确实是自然数家族中最小的。
可别小看了这个最小的“1”,它是自然数的单位,是自然数中的第一代,人类最先认识的是“1”,有了“1”,才能得到1、2、3、4……
给你讲了万数之首“1”的特殊地位,所以,你千万别小看了它哦。
趣味数学故事(二)
说起数学的作用,我们说上一天一夜也说不完,没有数学,我们生活也很不方便。那么,你知道数学除了日常生活中的简单运算,还可以做什么?能像警察那样破案吗?可以的,不信看看侠盗亚森罗宾是怎样用数学破案的。
巴黎郊外有一座中世纪留下的古老城堡,其年代几乎与著名的“巴黎圣母院”同样久远,因而成了旅游观光的胜地,吸引了来自世界各地的游客。下面这则故事就是出自—位导游之口。
古堡的顶层有一座尘封的钟楼,里面住着一个怪人,唯一的对外通道是个走起来嘎嘎响、陡峭异常的木质楼梯,大约有几十级,但肯定不到一百级。
某日黄昏,怪人的四位互不相识的朋友阿列克赛、巴顿、克林、杜邦,几乎在同一时间先后来访。他们发现怪人已经被人杀害了,房间里面看起来很恐怖。当下四人大惊失色,争先恐后地拼命逃走。从脏乱不堪的狭窄楼梯(一次只能通过一人)跑下来,阿列克赛一步下2级台阶,巴顿一步下3级台阶,克林一步下4级台阶,而杜邦的本事最大,竟然一步能下5级台阶。
出事以后,侠盗亚森罗宾乔装成一名体面的上流社会绅士,自告奋勇地前来侦破此案。他发现,同时印下四个人脚印的台阶仅在最高处和最低处。
为了追查凶手,脚印混乱了就不好办,于是亚森罗宾特别重视只留有一个人脚印的台阶。后来的结果充分证明他的看法是正确无误的,最后终于抓获凶手,把他绳之以法。
现在要问你的是,通向钟楼的木楼梯上有多少级台阶只印下了一个人(不管是谁的)的脚印
答案:
由于4的倍数肯定是2的倍数,所以克林的情况可以不必考虑,这就省掉了一个人,2,3,4,5的最小公倍数是60,而60又小于100,所以钟楼的木楼梯共有60级台阶。
阿列克赛的脚印落在第2,4,6,8,l0,12,…,58,60级台阶上,但应排除2×3及其倍数的各级阶梯;同理,还需要排除4的倍数的各级阶梯和5的倍数的各级阶梯。于是剩下第2,14,22,26,34,38,46,58共八级。其一般形式为2×p(其中p=1,以及除去2、3、5以外的素数)。
巴顿的脚印落在第3,6,9,12,…,60级阶梯上,但应排除混有别人脚印的第6,12,15,18,……级阶梯,剩下第3,9,2l,27,33,39,51,57,共八级。
前面已经说过克林的情况可以不考虑了,最后再来看一下杜邦的情况。很明显,只留下他一个人脚印的阶梯是第5,25,35,55级,共四级。
所以,问题的答案是8+8+4=20级。
下册数学小报
1.36×(913-276÷23)
2.(93+25×21)×9
3.507÷13×63+498
4.723-(521+504)÷25
5.384÷12+23×371
6.(39-21)×(396÷6)
二、列式计算(20分)
1.96减去35的差,乘63与25的和,积是多少
2.2727除以9的商与36和43的积相差多少
3.3与9的差除336与474的和,商是多少
4.一个数比96与308的积多36,求这个数.
5.最大的两位数与最小的三位数的和与差的积是多少
三、判断(正确的括号中划“√”,错误的在括号中划“×”并改正)(15分)
1.720÷(15-3×2)
=720÷(12×2)
=720÷24
=30
2.3889-(108-931)×5
=3889-149×5
=3889-745
=3144
3.(800+200÷50)×3
=(100÷50)×3
=20×3
=60
四、填空(10分)
下面是小红各科考试成绩的统计图,根据统计图回答下列问题.
1.语文分、数学分、外语分.
2.数学比外语高分.
3.三科平均分.
五、应用题(31分)
1.一台磨面机每小时磨面800千克,照这样计算,6台磨面机5小时能磨面粉多少千克?(用两种方法解答)
2.一堆煤共800吨,用5辆卡车,16次可以运完,平均每辆卡车每次运几吨
3.一辆汽车6小时行了300千米,一列火车6小时行了600千米,火车比汽车每小时多行多少千米
4.向阳小学气象小组一周中,测得每天的最高气温分别为:31、31、34、32、33、30、33度.这一周最高平均气温是多少度
数学公式(上、下、续合并
hello!大家好!你们知道我是谁吗?我可是赫赫有名的数学大师(能别吹牛吗)!最近,经过我呕心沥血(你把心呕出来了还怎么写作文)、九九八十一天(嘻嘻,不好意思,其实只有一天)的研究,想出了一些新的数学公式——( )=( )等.只要在括号里填上文字或数字,公式就成立啦!你们没见过吧?我先给你介绍一种我想出的公式中最最基础的一种公式——( )=( )(献丑,献丑).
1.(作业不会做,问老妈)=(碰一鼻子灰)
一天,我回到家后,正在做老师布置的作业——作文.作文的题目是《我最喜爱的卡通明星》,老师让我们写米老鼠.该怎么写呢?我想着想着,老妈突然催我写得要快.于是,我想也没想就写了起来.第二天,老师说我写得不好,要重新写.回到家后,我不情愿地问老妈:"老师要求我们写一篇作文,题目是《我最喜爱的卡通明星》,该怎么写啊?"老妈满脸气愤地说:"自己写(其实她也不会写)!不要什么作业都问别人!这篇作文该怎么写啊?明天还要交给老师呢!"我轻声说.我这话竟然被老妈听见了.可怜的我听到了一声"母狮子"的超级"狮吼":"本来就是你不对,你竟然还敢反驳?小心我罚你打扫一个月的厕所……"天哪,老妈"我立刻捂住耳朵,逃进了"(厕所)".
2.(上课不认真听课)=(我倒霉)
一天,在上英语(我觉得英语是最无聊的科目)时,我心不在焉,没有认真听课,所以我根本不知道老师在讲什么."叮铃铃……"下课铃响了,英语老师让我们把已经讲解完并且已经订正完的考卷交上讲台.到了下午的活动课时,英语老师叫去她的办公室.到了"牢房",老师对我说:"我在上课时把考卷全部讲解了一遍,可你的订正竟然还是错的!我……我……我……"我下得一身冷汗,说不出话来.紧接着,又是一声"惊天动地狮吼":"我什么我?赶快给我一张纸,我会把你的情况写在上面的,记住,一定要家长签字!明天我要是没有看到你的卷子上的签字,你就把这个张考卷抄一百遍,要是在学校抄不完就别回家!"(我自言自语:我妈这"母狮子"最凶了,要她签字,我的"pp(屁股)"肯定要受虐待啦)
3.(我的腿摔伤了)=(我掺叫)
一天,我们家刚吃好饭,老爸说:"刚吃完饭时要散散步,这样对身体有好处!"我和老妈都表示同意.于是,我和老爸、老妈正在公寓里的喷泉边散步.走着走着,我突然摔倒了.老爸连忙跑过来,看了看我的伤口.他发现我的腿破了.因为他怕时间长了,我的伤口会感染,所以,他和老妈以"飞毛腿"的速度带我去了医院.到了医院后,医生说我需要缝针.我顿时吓坏了,差点连尿都快出来了.你知道我为什么会这么害怕么?缝针可是很疼的啊!可我还没来得及把抱怨说出口,就被医生抬上了床."白医杀手":"只要缝一针,一点也不疼哦!"我还没把"不"说出口,"白医杀手"就凶狠地把一针缝了下去……"好——疼——呀——"医院里传出了我的一声掺叫,叫声经久不息……
你们是不是特别想知道本大师还会给大家介绍什么公式?告诉你们吧,这次我要给你们介绍的公式是——( )÷( )=( ).这公式你们见过吗?什么?你们说你们没见过?嗨,真没见识!还是我来给你们介绍一下吧!
1.(作业)÷(2)=(我快乐)
一天,语文老师上完了课,对我们说:"经过我校教导处最新讨论,我们几位语文老师提议:今天开始,作业一律减少一半.除了"布置作业狂"前三王(我们学校最喜欢布置作业的三位老师)以外,老师们全部支持这个提议,少数服从多数,今天起,作业一律减少一半!"耶!"全班欢呼一片.我突然看到平时上课最喜欢布置作业而且也最凶的秦老师正在失望地叹着气.你们知道为什么吗?还不是因为她名列全校"布置作业狂"前三王,校长警告她:要是发布这条消息后,还布置那么多作业,就把她从教师名单中开除!所以她现在再也不敢布置那么多作业了.她本来每天都要布置一课一练、数学题十道、一张数学试卷.现在,她每天只布置一课一练.回到家后,想我这种做作业速度一流的同学,回家后十分钟就能把作业做完.我做完作业后,不是看电视就是上网,真是"very happy".
2.(上网时间)÷(2)=(我难过)
一天,老妈发现我的视力从0点8跌到了0点5.跌的全部时间竟然还不到一个月.真是比股票跌得还快!于是性格果断老妈当机立断,对我公布了一条消息:"由于你视力逐渐下降,所以嘛……从今天起,你的上网就减少一半吧!你可不能怪我呀,我也是为了你好嘛(为我好可以,但能不能换一种方式呀).你要是没事情干的话,你老妈我就亲自和你下象棋(拜托,您会下吗)!可是……"我想和老妈进行谈判(我可是"谈判高手".有一次,我用了一公斤口水,把老师扣的一分清洁分加了上去,这一分一加,我就从班级第二名边成了班级第一名).可是老妈的态度也很坚决,毫不留情地说:"这件事不能谈判!"啊?我本来每天能上时间有四十分钟,现在呢……只有二十分钟了!呜呜呜……
3.(打我的人)÷(2)=(我减少了一半痛苦)
一天,我的英语考试成绩很差(具体分数不透露),我就变成了"沙包(被打)".我的老爸和老妈知道了这几乎可以让人晕倒的成绩,立刻气得咬牙切齿,立刻决定来个"男(老爸)女(老妈)混合双打".可是我的老爸正在北京出差.于是,"男女混合双打"变成了"女(老妈)单打".虽然还是要被打,但是"单打"至少比"双打"减少了一半痛苦啊!对了,不能再多说了,那位"母狮"已经朝我扑来啦……
我的知识渊博吧?如果我把这些"经典"的公式去申请专利,我一定会成为富翁(观众:真是财迷)!什么?你说有人要抢我的专利?岂有此理,看我"旋风脚"……
(十分钟后)我费了九牛二虎之力才好不容易才把那个想抢我的专利的人抓住.真是累死我了……对了,我还有一个数学公式没给你们介绍呢!那就是——( )×( )=( ).
1.(作业)×(2)=(我想……退休)
一天,我们班教了两篇课文.这两篇课文要抄的词语很多,所以……"今天的作业是:一课一练、1号本、语文写字本……"唉,咱班的语文老师又在不知厌倦地公布回家作业了.看来,今天晚上是甭想上网或看电视喽!可怜的我先做1号本,再做语文写字本,真是忙得不亦乐乎哇!唉,这么多作业我什么时候才能写完啊?我的天……
2.(金币)×(100)=(我发大财)
一天,我在晚上做了一个梦……我来到了"富翁国",国王给了我许多金币.我数了一下,一共有九九八十一枚呢(观众:你也太贪财了吧,连做梦都想着金币!对了,能不能分给我十个金币)!如果再乘以100,就有八千一百个金币啦!哈哈哈……"叮铃铃……"闹钟突然响了起来.咦,金币怎么都不见啦
3.(科学技术)×(2)=(生活便利、环保)
一天,我坐在公共汽车上,看见车后面排出的废气,忽然突发奇想:如果有一种新形汽车,是用太阳能前进,就不需要废气啦!还有一天,我坐在火车上,准备外出旅游,我突然觉得火车开得很慢,要是有一种速度非常非常快,在一秒钟之内就能环球旅行,那该多好呀!如果科学技术发达了,那么生活就能便利、环保啦!
大家快为我的研究成果掌声鼓励吧!
数学公式
一、小学数学周长、面积、体积计算公式:
1、长方形的周长=(长+宽)×2C=(a+b)×2
2、长方形的面积=长×宽S=ab
3、正方形的周长=边长×4C=a×4
4、正方形的面积=边长×边长S=a·a=a2
5、三角形的面积=底×高÷2S=ah÷2
6、平行四边形的面积=底×高S=ah
7、梯形的面积=(上底+下底)×高÷2S=(a+b)h÷2
8、直径=半径×2d=2r
半径=直径÷2r=d÷2
9、圆的周长=圆周率×直径=圆周率×半径×2C=πd=2πr
10、圆的面积=圆周率×半径×半径
S=πr2
S=π(d÷2)2
S=π(C÷π÷2)2
11、长方体的棱长之和=(长+宽+高)×4
12、长方体的表面积=(长×宽+长×高+宽×高)×2
13、长方体的体积=长×宽×高公式:V=abh
14、正方体的棱长之和=棱长×12
15、正方体的表面积=棱长×棱长×6S=6a2
16、正方体的体积=棱长×棱长×棱长V=a·a·a=a3
17、长方体(或正方体)的体积=底面积×高
V=Sh=abh
18、圆柱的侧面积=底面周长×高
S侧=Ch=πdh=2πrh
19、圆柱的表面积=侧面积+底面积×2
S表=S侧+2S圆
已知r、hS表=2πrh+2πr2
已知d、hS表=πdh+2π(d÷2)2
已知C、hS表=Ch+2π(C÷π÷2)2
20、圆柱的体积=底面积×高
已知r、hV=Sh=πr2h
已知d、hV=π(d÷2)2h
已知C、hV=π(C÷π÷2)2h
21、圆锥的体积=1/3底面积×高。
V=1/3Sh=1/3πr2h
V=1/3π(d÷2)2h
V=1/3π(C÷π÷2)2h
22、三角形的任意两边之和大于第三边
23、三角形具有稳定性。
24、三角形的内角和是180°。
25、长方体、正方体都有6个面,12条棱,8个顶点。
26、长方形有2条对称轴,正方形有4条对称轴,圆有无数条对称轴。
27、平移、轴对称、旋转不改变图形的形状和大小;图形的放大与缩小只改变大小,不改变形状。
28、条形统计图——表示各种数量的多少。
29、折线统计图——反映数量的增减变化情况。
30、扇形统计图——反映各部分数量和总数间的关系。
31、三角形:
(1)按角分类:锐角三角形、直角三角形、钝角三角形。
(2)按边分类:一般三角形、等腰三角形、等边三角形。
顶角是60o的等腰三角形一定是(等边)三角形。
有两个角是45o的角一定是(直角)三角形。
32、把一个长方形拉成平行四边形,周长(不变),面积(变小)。
把一个平行四边形拉成长方形,周长(不变),面积(变大)。
33、圆的半径扩大2倍,它的周长扩大(2)倍,面积扩大(4)倍。
任何圆的周长是直径的(π)倍。
34、长方体的长、宽、高(或正方体的棱长)都变为原来的2倍,那么它的总棱长也扩大到原来的2倍,面积会扩大到原来的4倍,体积会扩大到原来的8倍。
长方体的长、宽、高(或正方体的棱长)都变为原来的3倍,那么它的总棱长也扩大到原来的3倍,面积会扩大到原来的9倍,体积会扩大到原来的27倍。
面积是平方倍体积是立方倍
35、π=3.142π=6.283π=9.42
4π=12.565π=15.76π=18.84
7π=21.988π=25.129π=28.26
36、圆柱的体积是与它等底等高的圆锥的(3倍)。把一个圆柱形木块削成一个最大的圆锥,把圆锥体积看成(1份),可把削去部分的体积看成(2份),圆柱的体积就有这样的(3份)。
二、算术方面
1、加法交换律:两数相加交换加数的位置,和不变。
a+b=b+a
2、加法结合律:三个数相加,先把前两个数相加,或先把后两个数相加,再同第三个数相加,和不变。
(a+b)+c=a+(b+c)
3、乘法交换律:两数相乘,交换因数的位置,积不变。
a×b=b×a
4、乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,再和第三个数相乘,它们的积不变。
(a×b)×c=a×(b×c)
5、乘法分配律:两个数的和同一个数相乘,可以把两个加数分别同这个数相乘,再把两个积相加,结果不变。
(a+b)×c=a×c+b×c
6、减法性质:
(1)a-b-c=a-(b+c)
(2)a-b-c=a-c-b
7、除法性质:
(1)a÷(b×c)=a÷b÷c
(2)a÷(b÷c)=a÷b×c
8、在除法里,被除数和除数同时扩大(或缩小)相同的倍数,商不变。
9、0除以任何不是0的数都得0。
10、2的倍数特征是:个位上是0,2,4,6或8
11、5的倍数特征是:个位上是0或5。
12、3的倍数特征是:各个数位上的数字之和是3的倍数。
13、最小的偶数是(0)最小的奇数是(1)。
14、最小的质数是(2),最小的合数是(4)。
15、奇数+奇数=偶数
偶数+偶数+偶数
奇数+偶数=奇数
16、奇数×奇数=奇数
奇数×偶数=偶数
偶数×偶数=偶数
17、分数的加、减法则:同分母的分数相加减,只把分子相加减,分母不变。异分母的分数相加减,先通分,然后再加减。
18、分数的乘法法则:用分子的积做分子,用分母的积做分母。
19、分数的除法法则:除以一个数(0除外)等于乘以这个数的倒数。
20、
21、比:两个数相除就叫做两个数的比。
比的前项和后项同时乘以或除以一个相同的数(0除外),比值不变。
22、比例:表示两个比相等的式子叫做比例。如3:6=9:18
在比例里,两外项之积等于两内项之积。
23、正比例:两种相关联的量,一种量变化,另一种量也随着化,如果这两种量中相对应的的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系。
y/x=k(k一定)或kx=y
24、反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关系。
x·y=k(k一定)或k/x=y
25、(1)图上距离:实际距离=比例尺或
(2)实际距离=图上距离÷比例尺
(3)图上距离=实际距离×比例尺
26、鸽巢问题:物体数÷抽屉数=商……余数
至少数:商+1
27、自行车问题:
(1)前齿轮齿数×前齿轮转数=后齿轮齿数×后齿轮转数
(2)自行车蹬一圈走的距离=
28、等式:等号左边的数值与等号右边的数值相等的式子叫做等式。等式的基本性质:等式两边同时乘以(或除以)一个相同的数(不为0),等式仍然成立。
29、方程式:含有未知数的等式叫方程式。
30、一元一次方程式:含有一个未知数,并且未知数的次数是一次的等式叫做一元一次方程式。
31、分数:把单位“1”平均分成若干份,表示这样的一份或几份的数,叫做分数。
32、分数的加减法则:同分母的分数相加减,只把分子相加减,分母不变。异分母的分数相加减,先通分,然后再加减。
33、分数大小的比较:同分母的分数相比较,分子大的大,分子小的小。异分母的分数相比较,先通分然后再比较;若分子相同,分母大的反而小。
34、分数乘整数,用分数的分子和整数相乘的积作分子,分母不变。
35、分数乘分数,用分子相乘的积作分子,分母相乘的积作为分母。
36、分数除以整数(0除外),等于分数乘以这个整数的倒数。
37、真分数:分子比分母小的分数叫做真分数。真分数1。
38、假分数:分子比分母大或者分子和分母相等的分数叫做假分数。假分数≥1。
39、带分数:把假分数写成整数和真分数的形式,叫做带分数。
带分数>1。
40、分数的基本性质:分数的分子和分母同时乘以或除以同一个数(0除外),分数的大小不变。
41、一个数除以分数,等于这个数乘以分数的倒数。
42、甲数除以乙数(0除外),等于甲数乘以乙数的倒数。
43、中位数:按顺序排列后,最中间的一个数(奇数个)或最中间两个数的平均数(偶数个)。
44、众数:表示一组数据中出现次数最多的那个数。
45、一个数的因数的个数是有限的,它的最小的因数是1,最大因数是它本身,一个数的倍数的个数是无限的,最小倍数是它本身。
46、=0.2=0.4=0.6=0.8
1a
2
=0.25=0.75=0.125=0.375
=0.625=0.875=0.5
47、0既不是正数也不是负数,0是正数和负数的分界点。
负数<0<正数
两个负数比较,负号后面的数越大这个数反而越小。-6.8<-0.4-2>-10
48、小数点右边第一位是(十分位),计数单位是(十分之一);第二位是(百分位),计数单位是(百分之一),第三位是(千分位),计数单位是(千分之一)……
49、(1)相邻的两个数一定互质。(如8和9)
(2)1和任何正整数都互质。(如1和8)
(3)如果两个数是倍数关系,那么较小数就是这两个数的最大公因数;较大数就是这两个数的最小公倍数。
如:6和24的最大公因数是6,最小公倍数是24。
(4)如果两个数是互质关系,它们的最大公因数就是1;最小公倍数就是它们的积。
如:4和15的最大公因数是(1);最小公倍数是(60)。
50、为了读写方便,常常把较大的数改写成用“万”或“亿”作单位的数。
如只要求“改写”,结果应是准确数。如:768000000=(7.68)亿
如要求“省略”万(亿)后面的尾数,结果应是近似数。
如:768000000≈(8)亿
51、小数的性质:小数的末尾添上0或者去掉0,小数的大小不变。
52、小数点向右移动一位、两位、三位……原数就扩大到原来的10倍、100倍、1000倍,……小数点向左移动一位、两位、三位……原数就缩小到原来的1/10、1/100、1/1000……
三、单位换算
1、1千米=1000米
1米=10分米=100厘米=1000毫米
1分米=10厘米=100毫米
1厘米=10毫米
2、1平方米=100平方分米=10000平方厘米
1平方分米=100平方厘米
1平方厘米=100平方毫米
3、1立方米=1000立方分米
1立方分米=1000立方厘米
1立方厘米=1000立方毫米
4、1升=1立方分米=1000毫升
1毫升=1立方厘米
1升=1立方分米
5、1吨=1000千克
1千克=1000克
6、1公顷=10000平方米
1平方千米=100公顷=1000000平方米
1亩=666.666平方米
7、1元=10角=100分
1角=10分
8、1世纪=100年
1年=12月
1日=24小时
1时=60分
1分=60秒
1时=3600秒
9、大月(31天)有:1、3、5、7、8、10、12月
小月(30天)的有:4、6、9、11月
平年2月28天,闰年2月29天
平年全年365天,闰年366天
四、数量关系计算公式方面
1、每份数×份数=总数
总数÷每份数=份数
总数÷份数=每份数
2、速度×时间=路程
路程÷速度=时间
路程÷时间=速度
3、单价×数量=总价
总价÷单价=数量
总价÷数量=单价
4、工作效率×工作时间=工作总量
工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
5、加数+加数=和
和-一个加数=另一个加数
6、被减数-减数=差
被减数-差=减数
差+减数=被减数
7、因数×因数=积
积÷一个因数=另一个因数
8、被除数÷除数=商
被除数÷商=除数
商×除数=被除数
五、特殊问题
1、利润与折扣问题
利润=售价-成本
利润率=利润÷成本×100%=(售价÷成本-1)×100%
涨跌金额=本金×涨跌百分比
结余=收入-支出
折扣=售价÷原价×100%(折扣<1)
利息=本金×利率×存期
本息和=本金+利息
2、工程问题
(1)工作效率×工作时间=工作总量
工作总量÷工作时间=工作效率
工作总量÷工作效率=工作时间
(2)用假设工作总量为“1”的方法解工程问题的公式:
1÷工作时间=单位时间内完成工作总量的几分之几
1÷单位时间能完成的几分之几=工作时间
3、相遇问题
相遇路程=速度和×相遇时间
相遇时间=相遇路程÷速度和
速度和=相遇路程÷相遇时间
4、追及问题
追及距离=速度差×追及时间
追及时间=追及距离÷速度差
速度差=追及距离÷追及时间
5、溶液问题
溶质的质量+水的质量=溶液的质量
溶质的质量÷溶液的质量×100%=浓度
溶液的质量×浓度=溶质的质量
溶质的质量÷浓度=溶液的质量
6、和差问题的公式
(和+差)÷2=大数
(和-差)÷2=小数
7、和倍问题
和÷(倍数-1)=小数
小数×倍数=大数
(或者和-小数=大数)
8、差倍问题
差÷(倍数-1)=小数
小数×倍数=大数
(或小数+差=大数)
9、植树问题
(1)非封闭线路上的植树问题主要可分为以下三种情形:
在非封闭线路的两端都要植树,那么:
棵数=段数+1=全长÷间隔长+1
全长=间隔长×(棵数-1)
间隔长=全长÷(棵数-1)
在非封闭线路的一端要植树,另一端不要植树,那么:
棵数=段数=全长÷间隔长
全长=间隔长×棵数
间隔长=全长÷棵数
在非封闭线路的两端都不要植树,那么:
棵数=段数-1=全长÷间隔长-1
全长=间隔长×(棵数+1)
间隔长=全长÷(棵数+1)
2封闭线路上的植树问题的数量关系如下
棵数=段数=全长÷间隔长
全长=间隔长×棵数
间隔长=全长÷棵数
10、流水问题
顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
静水速度=(顺流速度+逆流速度)÷2
水流速度=(顺流速度-逆流速度)÷2
数学所有公式
人教版小学数学公式大全
一、小学数学几何形体周长面积体积计算公式
长方形的周长=(长+宽)×2C=(a+b)×2
长方形的面积=长×宽S=ab
正方形的周长=边长×4C=4a
正方形的面积=边长×边长S=a×a
三角形的面积=底×高÷2.S=a×h÷2
平行四边形的面积=底×高S=a×h
梯形的面积=(上底+下底)×高÷2S=(a+b)h÷2
直径=半径×2d=2r半径=直径÷2r=d÷2
圆的周长=圆周率×直径=圆周率×半径×2c=πd=2πr
圆的面积=圆周率×半径×半径
内角和:三角形的内角和=180度.
长方体的体积=长×宽×高公式:V=abh
长方体(或正方体)的体积=底面积×高公式:V=abh
正方体的体积=棱长×棱长×棱长公式:V=aaa
圆的周长=直径×π公式:L=πd=2πr
圆的面积=半径×半径×π公式:S=πr2
圆柱的表(侧)面积:圆柱的表(侧)面积等于底面的周长乘高.公式:S=ch=πdh=2πrh
圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积.公式:S=ch+2s=ch+2πr2
圆柱的体积:圆柱的体积等于底面积乘高.公式:V=Sh
圆锥的体积=底面×积高.公式:
分数的加、减法则:同分母的分数相加减,只把分子相加减,分母不变.异分母的分数相加减,先通分,然后再加减.
分数的乘法则:用分子的积做分子,用分母的积做分母.
分数的除法则:除以一个数等于乘以这个数的倒数.
二、单位换算
(1)1公里=1千米1千米=1000米1米=10分米1分米=10厘米1厘米=10毫米
(2)1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米
(3)1立方米=1000立方分米1立方分米=1000立方厘米1立方厘米=1000立方毫米
(4)1吨=1000千克1千克=1000克=1公斤=2市斤(5)1公顷=10000平方米1亩=666.666平方米
(6)1升=1立方分米=1000毫升1毫升=1立方厘米
(7)1元=10角1角=10分1元=100分
(8)1世纪=100年1年=12月大月(31天)有:135781012月小月(30天)的有:46911月
平年2月28天,闰年2月29天平年全年365天,闰年全年366天1日=24小时1时=60分
1分=60秒1时=3600秒
三、数量关系计算公式方面
1、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数2、1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数3、速度×时间=路程路程÷速度=时间路程÷时间=速度4、单价×数量=总价总价÷单价=数量总价÷数量=单价5、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率
6、加数+加数=和和-一个加数=另一个加数
7、被减数-减数=差被减数-差=减数差+减数=被减数8、因数×因数=积积÷一个因数=另一个因数
9、被除数÷除数=商被除数÷商=除数商×除数=被除数
四、算术方面
1.加法交换律:两数相加交换加数的位置,和不变.
2.加法结合律:三个数相加,先把前两个数相加,或先把后两个数相加,再同第三个数相加,和不变.
3.乘法交换律:两数相乘,交换因数的位置,积不变.
4.乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,再和第三个数相乘,它们的积不变.
5.乘法分配律:两个数的和同一个数相乘,可以把两个加数分别同这个数相乘,再把两个积相加,结果不变.如:(2+4)×5=2×5+4×5.6.除法的性质:在除法里,被除数和除数同时扩大(或缩小)相同的倍数,商不变.0除以任何不是0的数都得0.
7.等式:等号左边的数值与等号右边的数值相等的式子叫做等式.等式的基本性质:等式两边同时乘以(或除以)一个相同的数,等式仍然成立.8.方程式:含有未知数的等式叫方程式.
9.一元一次方程式:含有一个未知数,并且未知数的次数是一次的等式叫做一元一次方程式.
学会一元一次方程式的例法及计算.即例出代有χ的算式并计算.10.分数:把单位“1”平均分成若干份,表示这样的一份或几分的数,叫做分数.11.分数的加减法则:同分母的分数相加减,只把分子相加减,分母不变.异分母的分数相加减,先通分,然后再加减.
12.分数大小的比较:同分母的分数相比较,分子大的大,分子小的小.异分母的分数相比较,先通分然后再比较;若分子相同,分母大的反而小.13.分数乘整数,用分数的分子和整数相乘的积作分子,分母不变.14.分数乘分数,用分子相乘的积作分子,分母相乘的积作为分母.15.分数除以整数(0除外),等于分数乘以这个整数的倒数.16.真分数:分子比分母小的分数叫做真分数.
17.假分数:分子比分母大或者分子和分母相等的分数叫做假分数.假分数大于或等于1.
18.带分数:把假分数写成整数和真分数的形式,叫做带分数.19.分数的基本性质:分数的分子和分母同时乘以或除以同一个数(0除外),分数的大小不变.
20.一个数除以分数,等于这个数乘以分数的倒数.
21.甲数除以乙数(0除外),等于甲数乘以乙数的倒数.
五、特殊问题
和差问题的公式
(和+差)÷2=大数
(和-差)÷2=小数
和倍问题
和÷(倍数-1)=小数
小数×倍数=大数
(或者和-小数=大数)
差倍问题
差÷(倍数-1)=小数
小数×倍数=大数
(或小数+差=大数)
植树问题
1非封闭线路上的植树问题主要可分为以下三种情形:
(1)如果在非封闭线路的两端都要植树,那么:
株数=段数+1=全长÷株距-1
全长=株距×(株数-1)
株距=全长÷(株数-1)
(2)如果在非封闭线路的一端要植树,另一端不要植树,那么:株数=段数=全长÷株距
全长=株距×株数
株距=全长÷株数
(3)如果在非封闭线路的两端都不要植树,那么:
株数=段数-1=全长÷株距-1
全长=株距×(株数+1)
株距=全长÷(株数+1)
2封闭线路上的植树问题的数量关系如下
株数=段数=全长÷株距
全长=株距×株数
株距=全长÷株数
盈亏问题
(盈+亏)÷两次分配量之差=参加分配的份数
(大盈-小盈)÷两次分配量之差=参加分配的份数
(大亏-小亏)÷两次分配量之差=参加分配的份数
相遇问题
相遇路程=速度和×相遇时间
相遇时间=相遇路程÷速度和
速度和=相遇路程÷相遇时间
追及问题
追及距离=速度差×追及时间
追及时间=追及距离÷速度差
速度差=追及距离÷追及时间
流水问题
(1)一般公式:
顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
静水速度=(顺流速度+逆流速度)÷2
水流速度=(顺流速度-逆流速度)÷2
(2)两船相向航行的公式:
甲船顺水速度+乙船逆水速度=甲船静水速度+乙船静水速度(3)两船同向航行的公式:
后(前)船静水速度-前(后)船静水速度=两船距离缩小(拉大)速度浓度问题
溶质的重量+溶剂的重量=溶液的重量
溶质的重量÷溶液的重量×100%=浓度
溶液的重量×浓度=溶质的重量
溶质的重量÷浓度=溶液的重量
利润与折扣问题
利润=售出价-成本
利润率=利润÷成本×100%=(售出价÷成本-1)×100%
涨跌金额=本金×涨跌百分比
折扣=实际售价÷原售价×100%(折扣<1)
利息=本金×利率×时间
税后利息=本金×利率×时间×(1-5%)
工程问题
(1)一般公式:
工作效率×工作时间=工作总量
工作总量÷工作时间=工作效率
工作总量÷工作效率=工作时间
(
1÷工作时间
÷单位时间能完成的几分之几2)用假设工作总量为“=单位时间内完成工作总量的几分之几1”的方法解工程问题的公式:=工作时间

