两个矩阵等价意味着什么(两矩阵等价有哪些性质)
朋友们,你好!今天我们来谈谈两个矩阵等价意味着什么,我知道大家对它有很多疑问,还有就是两矩阵等价有哪些性质,我相信也有很多人对它不够清楚。那么今天就一起来了解这两个问题吧!希望通过我的文章可以帮到你们,如果感觉有所解惑,欢迎大家关注本站,更新的内容会继续为大家解答,谢谢!
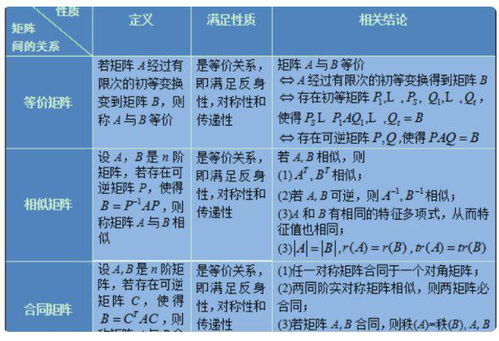
两个矩阵等价可以推出他们有着相同的行数以及列数并且它们的秩是相同的。
如果它们是同阶方阵,则它们所对应的行列式同时等于0或同时不等于0;5、可以通过有限次初等变换,由其中一个矩阵得到另外一个矩阵。扩展资料:在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合,最早来自于方程组的系数及常数所构成的方阵,这一概念由19世纪英国数学家凯利首先提出。矩阵等价是存在可逆矩阵,即A经过有限次的初等变换得到B。矩阵A和B等价,那么B和A也等价。矩阵等价的要求是:同一维度就可以了。比如三维你只要映射都映射到二维,我们就说矩阵等价。
以下内容供参考:电大作业网-等价矩阵
二、线性代数中两个向量组等价是什么意思
两个向量组可以互相线性表出,即是第一个向量组中的每个向量都能表示成第二个向量组的向量的线性组合,且第二个向量组中的每个向量都能表示成第一二个向量组的向量的线性组合。
向量组等价的基本判定是:两个向量组可以互相线性表示。
需要重点强调的是:等价的向量组的秩相等,但是秩相等的向量组不一定等价。
向量组A:a1,a2,…am与向量组B:b1,b2,…bn的等价秩相等条件是R(A)=R(B)=R(A,B),
其中A和B是向量组A和B所构成的矩阵。
向量组等价和矩阵等价是两个不同的概念。前者是从能够互相线性表出的角度给出定义;后者是从初等变换的角度给出定义。向量组(必须包含向量个数相同)等价能够推出矩阵等价。但是矩阵等价不一定能推出向量组等价。
向量组等价,是两向量组中的各向量,都可以用另一个向量组中的向量线性表示。
矩阵等价,是存在可逆变换(行变换或列变换,对应于1个可逆矩阵),使得一个矩阵之间可以相互转化。
如果是行变换,相当于两矩阵的列向量组是等价的。
如果是列变换,相当于两矩阵的行向量组是等价的。
由于矩阵的行秩,与列秩相等,就是矩阵的秩,在行列数都相等的情况下,两矩阵等价实际上就是秩相等,反过来,在这种行列数都相等情况下,秩相等,就说明两矩阵等价。
三、两矩阵等价有哪些性质
1,等价矩阵的性质:
2,矩阵A和A等价(反身性);
3,矩阵A和B等价,那么B和A也等价(等价性);
4,矩阵A和B等价,矩阵B和C等价,那么A和C等价(传递性);
5,矩阵A和B等价,那么IAI=KIBI。(K为非零常数)
6,具有行等价关系的矩阵所对应的线性方程组有相同的解
87,对于相同大小的两个矩形矩阵,它们的等价性也可以通过以下条件来表征:
(1)矩阵可以通过基本行和列操作的而彼此变换。
(2)当且仅当它们具有相同的秩时,两个矩阵是等价的。
扩展资料:
A进行一系列初等变换直到B,则A与B等价,即存在一个逆矩阵PQ,使B=PAQ,则AB秩相同。
AB的相似度是存在,但逆矩阵P使B=P-1ap,所以相似度结论强于等价性。
它们有更多的性质相同的特征值,相同的行列式
等价通常意味着你可以通过初等变换将它转换成另一个矩阵,本质上就是通过与另一个矩阵具有相同的秩。这是一个非常宽泛的条件。它并不适用于很多地方。
A和B很相似,有一个不变矩阵P,使得Pap^-1=B,这是线性代数或高等代数中最重要的关系,高等代数中有一半都在处理这个关系。相似导致等价。
参考资料来源:百度百科-等价矩阵

