矩阵相似特征值相等吗(两个矩阵特征值相同一定相似吗)

大家好，欢迎点击我们的文章。今天，我想和大家深入交流一下矩阵相似特征值相等吗的相关知识，也会谈及两个矩阵特征值相同一定相似吗的相关内容。如果你对这些还不太明白，那么这篇文章就是为你准备的。我希望能够帮你解决问题，那就让我们现在就开始吧！

一、两个矩阵特征值相同一定相似吗

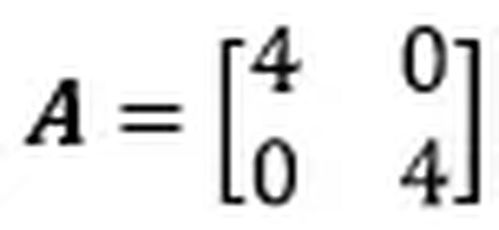
特征值相同，不一定相似，也不一定合同。

但是:

1）如果都是对称矩阵，那么特征值相同，能推出合同

2）如果两矩阵都可以相似对角化，则两矩阵特征值相同，能推出相似。

扩展资料：

在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。

矩阵运算在科学计算中非常重要，而矩阵的基本运算包括矩阵的加法，减法，数乘，转置，共轭和共轭转置。

加法

矩阵的加法满足下列运算律(A，B，C都是同型矩阵)：

应该注意的是只有同型矩阵之间才可以进行加法。

减法

数乘

矩阵的数乘满足以下运算律：

矩阵的加减法和矩阵的数乘合称矩阵的线性运算。

转置

把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵[9]，这一过程称为矩阵的转置

矩阵的转置满足以下运算律：；；

共轭

矩阵的共轭定义为:

.一个2×2复数矩阵的共轭如下所示：则

共轭转置

矩阵的共轭转置定义为：，也可以写为：。一个2×2复数矩阵的共轭如下所示：则

参考资料：百度百科-矩阵

二、特征值相等一定相似吗

两个矩阵的特征值相等的时候不一定相似

但当这两个矩阵是实对称矩阵时，有相同的特征值必相似

比如当矩阵A与B的特征值相同，A可对角化，但B不可以对角化时，A和B就不相似

比如如下两个矩阵

1 0 1 1

0 1和 0 1，

显然它们的特征值都是1，1

但是不能对角化，

因为1 1不能找到两个线性无关的特征向量

0 1

注意n阶矩阵A与对角阵相似的充要条件就是A有n个线性无关的特征向量，不能只看特征值

所以当这两个矩阵都是实对称矩阵时，都一定可以对角化，于是有相同的特征值就一定相似

这也就是我们的课本上一般只讨论对实对称阵进行对角化的原因，

对一般的矩阵讨论能否对角化比较复杂

三、相似矩阵的特征值相同为什么啊

假设x是矩阵A的特征值，那么有:xa=Aa

又因为A和B相似，所以有A=P^(-1)BP

将A=P^(-1)BP代入得到:xa=P^(-1)BPa

再将等式两边同时左乘P，得到Pxa=BPa

由于x是一个数，所以有x(Pa)=B(Pa)

由此可以证明x也是矩阵B的特征值，所以相似矩阵的特征值相同。

扩展资料

特征值是线性代数中的一个重要概念。在数学、物理学、化学、计算机等领域有着广泛的应用。设

A

是n阶方阵，如果存在数m和非零n维列向量 x，使得

Ax=mx

成立，则称

m

是A的一个特征值（characteristic

value)或本征值（eigenvalue)。非零n维列向量x称为矩阵A的属于（对应于）特征值m的特征向量或本征向量，简称A的特征向量或A的本征向量。

参考资料百度百科-特征值